В мире физики, где стремление к пониманию фундаментальных законов природы — это непрекращающийся поиск, теория струн выделяется как одна из наиболее амбициозных попыток объединить квантовую механику и гравитацию. Но что, если бы мы могли подойти к этому вопросу с другой стороны, не полагаясь на изначальные предположения, а скорее, выстраивая теорию «снизу вверх»?
Именно такой подход, известный как принцип бутстрапа, лежит в основе недавнего исследования, проливающего свет на уникальность теории струн и, в частности, амплитуды Венециано.В чем суть бутстрапа?
Представьте себе, что вы пытаетесь собрать пазл, не имея картинки на коробке. Принцип бутстрапа, в контексте физики, — это попытка построить теорию, исходя из минимального набора фундаментальных принципов, таких как лоренц-инвариантность (независимость физических законов от выбора инерциальной системы отсчета), локальность (взаимодействия происходят в точке) и унитарность (вероятность всех возможных событий равна 1). Вместо того чтобы строить теорию на основе каких-либо готовых «строительных блоков» вроде элементарных частиц, бутстрап концентрируется на свойствах наблюдаемых величин, таких как амплитуды рассеяния — вероятности того, как частицы будут взаимодействовать друг с другом. Этот подход открывает путь к созданию теории, опирающейся на самосогласованность и логику, а не на априорные предположения.

Амплитуда Венециано: ключ к разгадке
Амплитуда Венециано, предложенная в конце 1960-х годов, стала предвестником теории струн. Она описывает рассеяние адронов (частиц, участвующих в сильных взаимодействиях) и обладает рядом удивительных свойств. Одним из таких свойств является ее «мягкое» поведение при высоких энергиях — амплитуда не возрастает бесконечно, а наоборот, быстро затухает. Это поведение контрастирует с теориями точечных частиц, которые при высоких энергиях, как правило, демонстрируют расхождение.
В новом исследовании ученые задались вопросом: можно ли вывести амплитуду Венециано, отталкиваясь от принципа бутстрапа, не делая никаких предположений о струнах? Их результаты показывают, что да, это возможно. Более того, они показали, что амплитуда Венециано — это, по сути, единственное решение, удовлетворяющее определенным условиям.
Условия уникальности: «обрезание уровней» и симметрия
Два ключевых предположения, которые обеспечивают уникальность решения, связаны с поведением амплитуды при высоких энергиях и так называемым «обрезанием уровней». «Обрезание уровней» — это явление, при котором амплитуда ведет себя как рациональная функция (отношение многочленов) в особых точках импульса. Другими словами, при определенных значениях энергии и импульса, бесконечная сумма, описывающая амплитуду, сводится к конечному числу слагаемых. Это явление, характерное для теории струн, не возникает в теориях точечных частиц.
Второе важное условие — требование кроссинг-симметрии. Это условие диктует, что амплитуда рассеяния должна оставаться неизменной при перестановке каналов рассеяния. Иными словами, если мы меняем ролями частицы на входе и выходе, то результат процесса (вероятность) должен остаться тем же. Наложение этих двух условий в сочетании с требованием «мягкого» поведения при высоких энергиях и приводит к уникальному решению, которым является амплитуда Венециано.
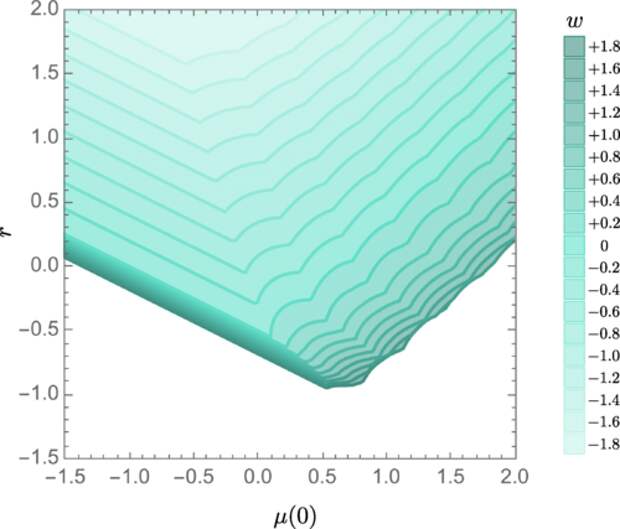
Спектр масс как продукт бутстрапа
Одним из самых интересных результатов исследования является то, что спектр масс (значения масс частиц) в теории не является входным параметром, а получается как результат из решения уравнений бутстрапа. Это означает, что принцип бутстрапа не только определяет форму амплитуды рассеяния, но и предсказывает характеристики частиц, которые участвуют в этих рассеяниях.
Что дальше?
Полученные результаты не только подтверждают уникальность амплитуды Венециано, но и открывают новые пути для исследования теории струн и, возможно, для построения единой теории всего. Ученые планируют обобщить этот подход на более сложные случаи, включая рассеяние нескольких частиц и гравитационные взаимодействия.
Смогут ли они, в итоге, найти полную и единую теорию, опираясь лишь на основные принципы и логику? Покажет время, но можно с уверенностью сказать, что принцип бутстрапа в сочетании с глубоким пониманием свойств струнных амплитуд, дает нам мощный инструмент для исследования глубин мироздания.
Свежие комментарии